|
Департамент освіти і науки, молоді та спорту Чернівецької обласної державної адміністрації Інститут післядипломної педагогічної освіти Чернівецької області Науково-методичний центр практичної психології і соціальної роботи ПОГОДЖЕННО ЗАТВЕРДЖЕНО За цих умов соціальна педагогіка, як особлива сфера професійної діяльності, стає значним чинником у системі допомоги широким верствам населення загалом і роботи соціального педагога з дітьми, батьки яких за кордоном, зокрема Диплом 0.6 Mb. 6 стр. |
читати |
|
О. В. Варецька Україна, м. Запоріжжя, КЗ «Запорізький обласний інститут післядипломної педагогічної освіти» ДУХОВНО-ЕКОНОМІЧНЕ ВИХОВАННЯ В ЄДИНОМУ ОСВІТНЬОМУ ПРОСТОРІ «СІМ’Я – ДНЗ – СУСПІЛЬСТВО» Диплом 138.86 Kb. 1 стр. |
читати |
|
Випуску: Надання першої медичної допомоги Українське незалежне інформаційне агентство новин (УНІАН). Засновано в березні 1993 року 0.59 Mb. 4 стр.     
|
читати |
|
ОКУЛЬТНА СУТНІСТЬ САТАНІЗМУ ТА ВІРОВЧЕННЯ ЛА ВЕЯ Сатанізм Асмодей, Сет та інші. При цьому нерідко перших трьох демонів вважають за одну особу в трьох іпостасях. Віра в існування Сатани (Диявола, Люцифера) виникла у релігіях стародавнього Ірану та в іудаїзмі, набула поширення в середньовічній Європі як результат розвитку християнської демонології 118.01 Kb. 1 стр. |
читати |
|
ЗАТВЕРДЖУЮ Робоча програма з навчальної дисципліни «Політична економія» для студентів за напрямом підготовки 030508 «Фінанси і кредит» 314.51 Kb. 4 стр. |
читати |
|
КАФЕДРА ФІНАНСІВ ТА БАНКІВСЬКОЇ СПРАВИ Взаємозв’язок фінансів з іншими категоріями: заробітною платою, ціною і кредитом 36.31 Kb. 1 стр. |
читати |
|
ПОДАТКОВИЙ КОДЕКС УКРАЇНИ Закону України від 5 липня 2012 року N 5083-VI, набирають чинності з 1 січня 2013 року Кодекс 9.95 Mb. 125 стр. |
читати |
 УКРАЇНА Чернівецька обласна державна адміністрація ДЕПАРТАМЕНТ ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНА Чернівецька обласна державна адміністрація ДЕПАРТАМЕНТ ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУГрушевського, 1; м. Чернівці, 58010; тел. (0380372) 55-29-66, факс (0380372) 57-32-84; e-mail 90.52 Kb. 1 стр. |
читати |
|
Сценарій "Новий рік вже на порозі" Прошу всіх налити келихи. Наше свято присвячене проводам старого 2012р розпочинається 294.4 Kb. 1 стр. |
читати |
|
КНИЖКОВА ПАЛАТА УКРАЇНИ Бібліотечна справа. Бібліотекознавство 5 030 Довідкові видання загального типу. Енциклопедії, словники тощо 5 1.1 Mb. 8 стр. |
читати |
 Вороніна Лариса Анатоліївна Вороніна Лариса АнатоліївнаМетод проектів як одна із форм інновацій у вихованні гармонійно розвиненої особистості через систему родинних цінностей 162.3 Kb. 1 стр. |
читати |
|
ВИПУСКУ: Щоб дитина повернулася з відпочинку здоровою 12 Українське незалежне інформаційне агентство новин (УНІАН). Засновано в березні 1993 року 0.84 Mb. 5 стр.     
|
читати |
|
Автор-упорядник: Хоменко Любов Василівна Посада: вчител ь світової літератури та російської мови Сьогодні, коли наша молода держава розбудовується, на уроках зарубіжної літератури, особливо в старших класах, стали надзвичайно актуальними україністичні студії 0.52 Mb. 4 стр.  
|
читати |
|
Уроку Основні засоби навчання: політична карта святу, картини, що відображають побут та культуру індійського народу, довідники, хрестоматії Урок 122.76 Kb. 1 стр. |
читати |
|
Черкаси на початку ХХ століття Доброго дня! Сьогодні ми здійснимо віртуальну подорож по місту Черкаси. Кожного дня ми ходимо вулицями нашого міста, їздимо транспортом, поспішаємо у своїх справах. Ми не задумуємося, як виглядало місто 100 років тому. Тож давайте здійсним мандрівку в минуле нашого древнього і вічно молодого міста 120.92 Kb. 1 стр.  
|
читати |
|
Українське незалежне інформаційне агентство новин (УНІАН). Засноване в березні 1993 року Генеральний директор Олег НАЛИВАЙКО. Головний редактор Олександр ХАРЧЕНКО тел. 279-31-31 0.73 Mb. 22 стр.  
|
читати |
|
ГАРЯЧИЙВ І СНИК №132 Об‘єднаного незалежного інформаційного центру в УНІАН Спільна ініціатива УНІАН, Міжнародного фонду «Відродження», Громадської коаліції «Новий вибір-2004», медіа-центру «Кандидат» 140.37 Kb. 1 стр. |
читати |
|
Розвиток освіти, літописання. Архітектура та образотворче мистецтво. Зміни в суспільному житті Галичини й Волині Мета: ознайомити учнів з культурною спадщиною Галицько-Волинської держави; вчити працювати з додатковими історичними джерелами, раціонально розподіляти час 108.06 Kb. 1 стр. |
читати |
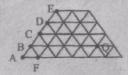 «Золотий ключик – 2006» 8 – 9 класи «Золотий ключик – 2006» 8 – 9 класиНа фізкультурному параді спортсмени спочатку вишикувалися так, що кількість спортсменів у кожній шерензі співпала з кількістю шеренг, а потім перешикувалися так, що кількість шеренг збільшилась на п'ять. На скільки зменшилась кількість спортсменів у кожній шерензі? 50.31 Kb. 1 стр. |
читати |
 ЧЕРКАСЬКИЙ ОБЛАСНИЙ ІНСТИТУТ ПІСЛЯДИПЛОМНОЇ ОСВІТИ ПЕДАГОГІЧНИХ ПРАЦІВНИКІВ ЧЕРКАСЬКИЙ ОБЛАСНИЙ ІНСТИТУТ ПІСЛЯДИПЛОМНОЇ ОСВІТИ ПЕДАГОГІЧНИХ ПРАЦІВНИКІВПроект профінансовано виконавчим агентством з освіти, аудівізуалізації та культури, яке діє на підставі повноважень, делегованих Європейською комісією Диплом 96.61 Kb. 1 стр. |
читати |
|
Орієнтовний план проведення консультацій з громадськістю на 2014 рік Питання або проект нормативно правового акта Соціальні групи населення та заінтересовані сторони, на які буде поширюватися дія рішення, прийнятого за результатами консультацій 93.38 Kb. 1 стр. |
читати |
|
Про виконання соціальних ініціатив Президента України щодо вдосконалення роботи соціальних служб шляхом повного охоплення соціальними послугами вразливих Про виконання соціальних ініціатив Президента України щодо вдосконалення роботи соціальних служб шляхом повного охоплення соціальними послугами вразливих категорій населення, раннього виявлення проблемних сімей та своєчасного надання їм підтримки 64.85 Kb. 1 стр. |
читати |
|
Підтверджую ідентичність електронної та паперової форм інформації, що подається до Комісії, та достовірність інформації, наданої для розкриття в Підтверджую ідентичність електронної та паперової форм інформації, що подається до Комісії, та достовірність інформації, наданої для розкриття в загальнодоступній інформаційній базі даних Комісії 198.64 Kb. 4 стр. |
читати |
|
Економічні науки Гладкий, Олександр Віталійович. Менеджмент регіонального розвитку : навч посіб. / О. В. Гладкий. – К. Академвидав, 2013. – 248 с. – (Альма-матер). – Гриф МОН МС України (лист №1/11-10839 від 21. 11. 2011 р.) 20.15 Kb. 1 стр. |
читати |
|
ЗАТВЕРДЖУЮ Робоча програма з навчальної дисципліни «Економіка та бізнес» для студентів за напрямом підготовки 050101 «Комп'ютерні науки» 192.78 Kb. 1 стр. |
читати |
|
Тема: Поняття та основні ознаки підприємництва. Закон України Про підприємництво Мета Тема: Поняття та основні ознаки підприємництва. Закон України Про підприємництво Закон 63.17 Kb. 1 стр. |
читати |
|
Тема: Види та організаційно-правові форми торговельних підприємств Мета Природно, що виробниче підприємництво має бути прибутковим, відшкодовувати зроблені витрати. Вважають, що організація нового виробництва є доцільною лише в тому разі, якщо річний прибуток становитиме в сумі не менше ніж 15—20 від потрібних витрат 54.18 Kb. 1 стр. |
читати |
|
ЗАТВЕРДЖУЮ 52.46 Kb. 1 стр. |
читати |
|
ЗАТВЕРДЖЕНО Наказ Державного комітету України з питань регуляторної політики та підприємництва 09. 0 2004 N 65 У найменуванні юридичної особи зазначаються її організаційно-правова форма (крім органів державної влади, органів місцевого самоврядування, органів влади Автономної Республіки Крим) та назва. Найменування юридичної особи викладається державною мовою 34.67 Kb. 1 стр. |
читати |
|
Положення про оренду окремих елементів благоустрою міста для розміщення дитячих атракціонів, лу на парків, циркових вистав та пересувних малих архітектурних форм для здійснення підприємницької діяльності Положення розроблено на пiдставi Законів України "Про місцеве самоврядування в Україні", "Про оренду державного та комунального майна" 157.91 Kb. 1 стр. |
читати |
Додайте кнопку на своєму сайті:
При копіюванні матеріалу обов'язкове зазначення активного посилання © 2013
звернутися до адміністрації
bibl.com.ua
звернутися до адміністрації
bibl.com.ua